자료구조
1. 선형 구조(Linear Structure)
(1) 배열(Array)
- 정적인 자료 구조로 기억장소의 추가가 어렵고 메모리의 낭비가 발생함
- 크기, 형(type)이 동일한 자료를 순서대로 나열
- 반복적인 데이터 처리 작업에 적합한 구조
- 데이터마다 동일한 이름의 변수를 사용해 처리가 간편함
(2) 스택(Stack)

- 리스트의 한쪽 끝 Top(스택포인터): 자료의 삽입, 삭제 작업이 이뤄지는 자료 구조
- 후입선출(LIFO; Last In First Out) 방식
활용
- Postfix 형태 수식 계산(레지스터)
- 컴파일러 이용한 언어 번역
- 재귀 프로그램의 순서 제어
- 인터럽트 발생 시 복귀 주소 기억시키는데 사용
(1.3.1)Overflow
기억공간이 모두 차 있는데 데이터를 삽입(push)하면 일어나는 현상
Top = Top+1 #스택포인터 증가
If Top > m then #(1) 포인터 > 스택 길이
Goto AA # overflow 발생(서브루틴)
Else #이외 (2)삽입
Stack(Top) <- Item
(1.3.2)Underflow
기억공간이 비어있어서 데이터가 없는데 삭제(pop)하면 일어나는 현상
If Top=0 #(1)Top=0이면 underflow
Then (underflow)
Else #(2) 이외 값 삭제하고,
{ Remove Stack(TOP)
Top = Top-1 #스택 포인터 감소
}
(3) 큐(Queue)

- 리스트의 포인터 Rear에서 삽입 작업, Front에서 삭제 작업이 이뤄지는 자료 구조
- 선입선출(FIFO;First In First Out) 방식
- 운영체제의 작업 스케줄링
(4) 데크(Deque, Double Ended Queue)

- 리스트의 양쪽 끝에서 삽입, 삭제 작업을 할 수 있는 자료 구조
(5) 선형 리스트(Linear List)
(5.1) 연속 리스트(Contiguous List)
- 배열과 같이 연속되는 기억장소에 저장되는 자료 구조
- 기억장소를 연속적으로 배정받아, 기억장소 이용 효율은 밀도가 1로서 가장 좋음
- 중간에 데이터를 삽입하기 위해 연속된 빈 공간이 있어야함
- 삽입, 삭제 시 자료의 이동이 필요함
(5.2) 연결 리스트(Linked List)

- 자료들을 반드시 연속적으로 배열시키지 않고 임의의 기억공간을 기억시키되, 자료 항목의 순서에 따라 노드의 포인터 부분을 이용해 서로 연결시킨 자료 구조
- 노드의 삽입, 삭제 작업이 용이
- 기억공간이 연속적으로 놓여 있지 않아도 저장가능
- 연결을 위한 포인터가 필요하기 때문에 순차 리스트에 비해 기억 공간의 효율이 좋지 않음
- 연결을 위한 포인터를 찾는 시간이 필요하기 때문에 접근 속도가 느림
- 중간 노드 연결이 끊어지면 그 다음 노드를 찾기 힘듦
- 희소 행렬 -> Linked list (기억장소 절약)
2. 비선형 구조
(1) 트리(Tree)
(1) 구조
- 정점(Node),선분(Branch)을 이용해 사이클 없는 그래프(Graph)의 특수한 형태(관계=계층)
- 노드(Node): 트리의 기본 요소, 자료 항목과 다른 항목에 대한 가지(Branch)를 합친 것
- 근 노드/뿌리(Root Node): 트리의 맨 위에 있는 노드
- 단말 노드(Terminal Node): 자식이 하나도 없는 노드, Degree가 0인 노드
- 자식 노드(Son Node): 어떤 노드에 연결된 다음 레벨의 노드들
- 부모 노드(Parent Node): 어떤 노드에 연결된 이전 레벨의 노드들
- 형제 노드(Brother Node, Sibling): 동일한 부모를 갖는 노드들
- 디그리(Degree,): 각 노드에서 뻗어 나온 가지의 수
- 트리의 디그리: 트리 내 노드들의 디그리 중에서 가장 많은 수
eg.
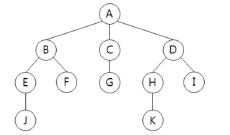
트리의 차수(Degree): 3개 (A의 자식 노드 B,C,D로 전체 트리에서 제일 차수가 높음)
트리의 단말 노드(Terminal): 5 개(J F G K I 는 자식이 하나도 없는 노드)
트리 순회방법 20년 1, 2, 3회
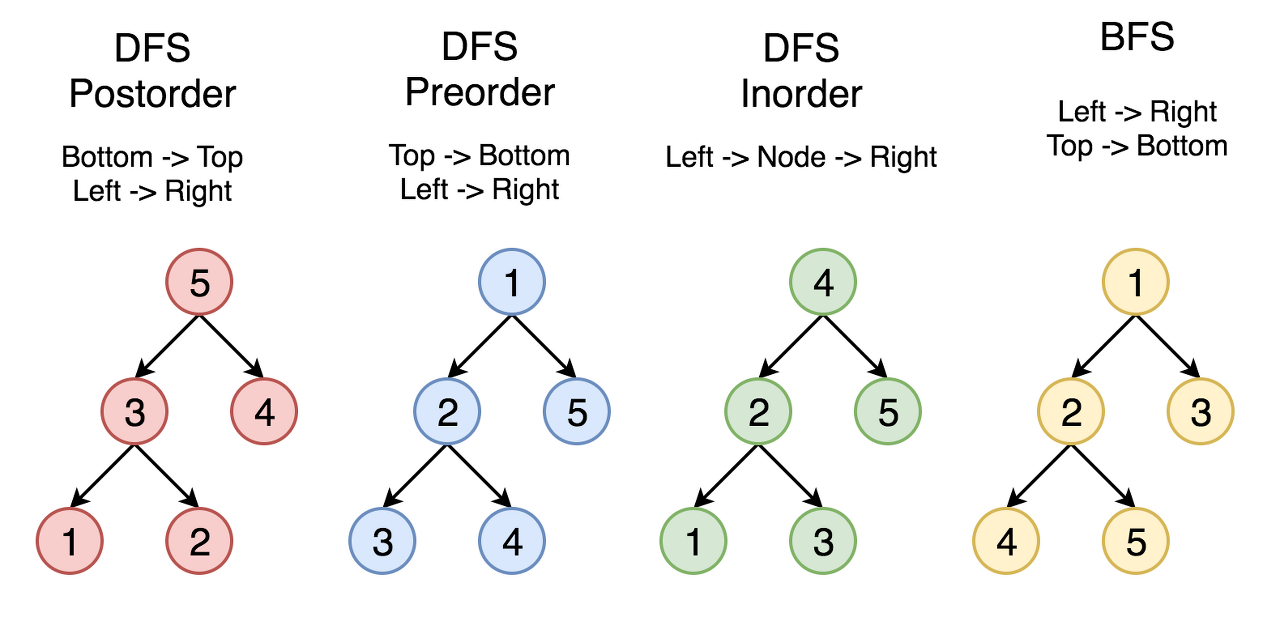
1) 깊이 우선 탐색 DFS(Depth First Search)
순환 알고리즘 형태로 재귀나 스택으로 구현
- Preorder(전위순회):Root-> Left -> Right
- Inorder(중위순회):Left->Root ->Right
- Postorder(후위순회):Left -> Right->Root
2) 넓이 우선 탐색(BFS (Breadth-First Search)
- 인접한 노드들을 먼저 탐색
- 최단 경로 탐색
쉽게 외우는 방법으로 하단과 같이 같은 색상 점끼리 연결해서 순서를 알아내는 방법도 있습니다.
(2) 그래프(Graph)
- 정점, 간선의 두 집합
(2.1)방향 그래프(Directed Graph)
- 정점을 연결하는 선에 방향이 있는 그래프
- n개의 정점으로 구성된 방향 그래프의 최대 간선 수 = n(n-1)
(2.2) 무방향 그래프(Undirected Graph)
- 정점을 연결하는 선에 방향이 없는 그래프
- n개의 정점으로 구성된 무방향 그래프의 최대 간선 수 = n(n-1)/2
(1) McCabe의 순환복잡도 20년 3회 기출문제
프로그램의 이해 난이도는 제어흐름 난이도의 복잡도에 따라 결정되며, 복잡도를 cyclomatic수(region수,폐구간,그래프 영역)에 의해서 산정하는 방법
McCabe의 cyclomatic 수 V(G) = Edge(간선) – vertex(정점) + 2
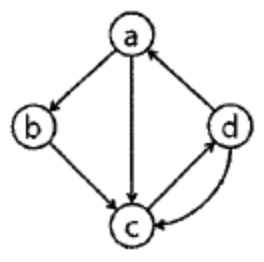
6개 선 - 4개 점 +2 =4
인접행렬
- 그래프의 방향 간선이 있으면 행렬의 P0=1, 인접하지 않으면 0

[정보처리기사] 개정된 정보처리기사 필기 목차
정처기 필기 100문제 중 각 챕터 당 20문제로 구성됩니다. 출판사 시나공의 정보처리기사 교재와 이전 기출문제들을 참고로 하여 간단히 키워드로요약하여 작성하였습니다. 각 중요도에 따라서
potato-potahto.tistory.com
'Challenges > 정보처리기사' 카테고리의 다른 글
| [정보처리기사]2.소프트웨어 개발/통합 구현/개발 지원 도구 (0) | 2021.08.23 |
|---|---|
| [정보처리기사]2.소프트웨어 개발/데이터 입·출력 구현/알고리즘 (0) | 2021.08.19 |
| [정보처리기사]1. 소프트웨어 설계/인터페이스 설계/인터페이스 방법 명세화 (0) | 2021.08.11 |
| [정보처리기사]1. 소프트웨어 설계/인터페이스 구현/미들웨서 솔루션 (0) | 2021.08.11 |
| [정보처리기사]1. 소프트웨어 설계/애플리케이션 설계/객체지향 분석 & 설계 (0) | 2021.08.10 |