지도학습 : 회귀분석(Regression Analysis)

1) 선형 회귀(Linear Regression):
연속형 관측값을 이용하여 연속형 수치 데이터를 선형 모델링통해 예측
가정: 반응변수와 독립변수와의 관계가 선형임을 가정(선형성,Linearity)
(1) 단순 선형 회귀(Simple Linear Regression)
하나의 설명/독립변수(explanatory variable x),하나의 반응/종속변수y사이의 관계 모델링, 특성과 타깃사이의 회귀 직선 관계를 나타내는 선형 방정식의 가중치 학습하여 예측

- β0 or w0: 절편(intercept)
- β1 or w1: slope 특성x의 가중치
- 잔차(Residuals): 실제 관측값과 예측값의 차이
- Regression line: 주어진 관측값에서 가장 적합한 라인
(2) 다중 선형 회귀(Multiple Linear Regression)
선형 회귀모델보다는 일반적으로 두개 이상의 설명/독립변수(explanatory variable x), 하나의 반응/종속변수y사이의 관계 모델링, 특성과 타깃사이의 회귀 직선 관계를 나타내는 선형 방정식의 가중치 학습하여 예측,
3 차원에서는 Regression line이 아닌 Regression Plane형태가 됨.( 3차원 이상은 그림으로 표현 불가)

최소제곱법 (Leaste Squareds method)
해당 독립변수(xi)에서의 각 관측값과 회귀선(Linear Regression)의 종속변수 값 yi의 차이의 제곱 합을 최소화(오차/잔차 최소화)하여 β 모수를 추정하는 방법으로 SSE 최소화
* 최소제곱법은 예측력을 보장하지 않음.
모수 회귀선

추정

경사하강법으로 회귀 모델의 파라미터 구하기
선형 회귀 모델의 적합성(fit of regression) 평가
(1)잔차 그래프(Residual Plot)- 선형 모델링이 적합한지 비선형 모델링이 적합한지 알아보기 위해 Residuald을 y축, 예측값x 축으로 표현

- 패턴 없음
- 이상치 (판단 기준이 있지만 범위에서 벗어남 ㅠㅠ ,Studentized Residual)
- 랜덤하게 분포( 평균 0, 등분산)
(2) 분산분석표 ANOVA Table: 평균 제곱 오차(Mean Squared Error,MSE)- 제곱 오차합(Sum Squared Error) 평균


훈련과 테스트 세트를 비교, 훈련세트 MSE < 테스트 MSE : 과대적합
(3) 결졍계수(Coefficient of determination, R2(R Squared) : 독립변수 변동으로 인해 설명되어지는 부분으로 0~1 사이 값 갖음
- R2 = 1 가까움 : MSE=0 , 완벽한 적합
- R2 = 0 가까움 : 변동 없음
- measure of fit but not prediction quality!!


시각화 이용 선형 관계 파악
산점도 행렬(Scatter Plot) - 데이터 이상치, 분포 파악(정규성 여부 파악),선형 관계 파악
상관관계 행렬(Correltion matrix) - 변수간의 선형 관계를 수치화 * pearson correltion 을 의미
- 0 가까움: 선형 관계가 약함
- |1| 가까움 : 양/음의 선형 관계가 강함
- + :양의 상관관계
- - : 음의 상관관계
비선형
(1) 특성변환
다항 회귀( Polynomial Regression):
각 독립변수에 n차수를 이용하여 다항식으로 표현
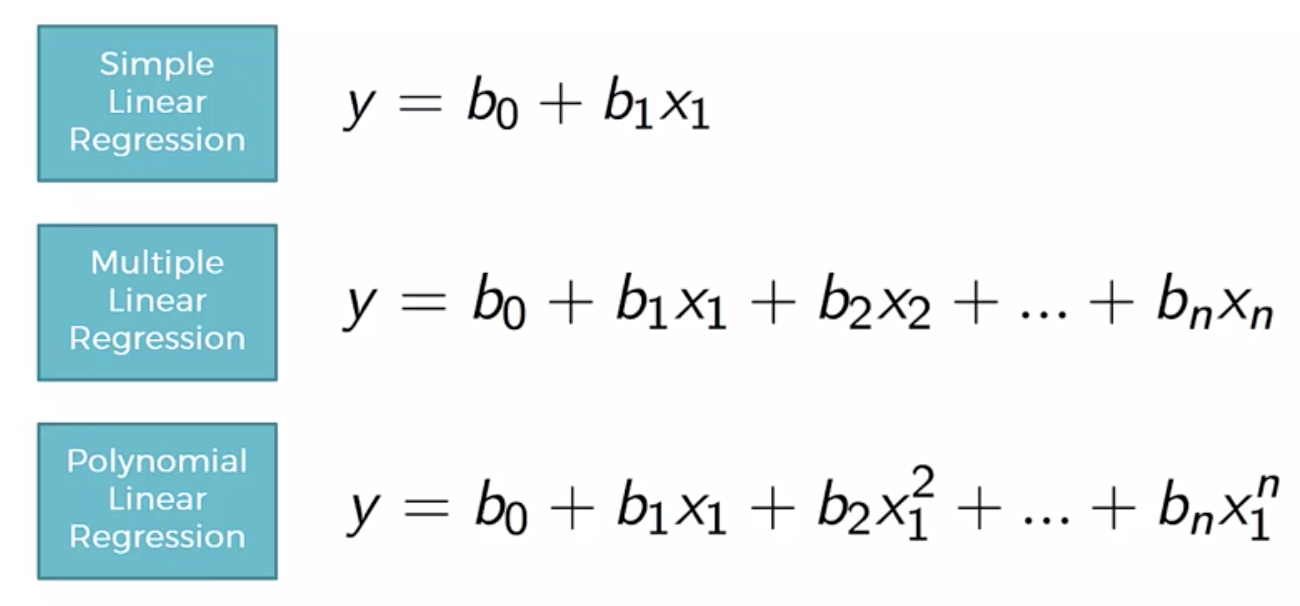

선형 회귀보다 다항 회귀가 훨씬 잘 표현함
과대적함 위험 증가, 모델 복잡도 증가
로그 (natural logatrithm) 변환
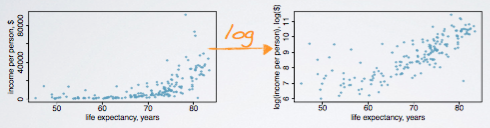
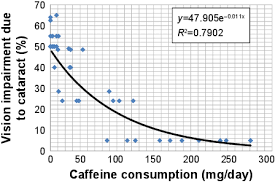
Reciplocal transformation
독립과 종속변수가 반비례관계(inversely related)
랜덤포레스트
Decision Tree 알고리즘 - 특성 변환 불필요, 정보 이득(IG)가 최대화 되는 특성 분할 결정하기 위해 불순도 지표 :엔트로피
랜덤포레스트: DT의 앙상블 방법으로 무작위성을 통해 일반화
정규화 Regularization
- 최적: 과적합 낮춤(적절한 편향에 분산을 줄임)
회귀 규제 Penalty :
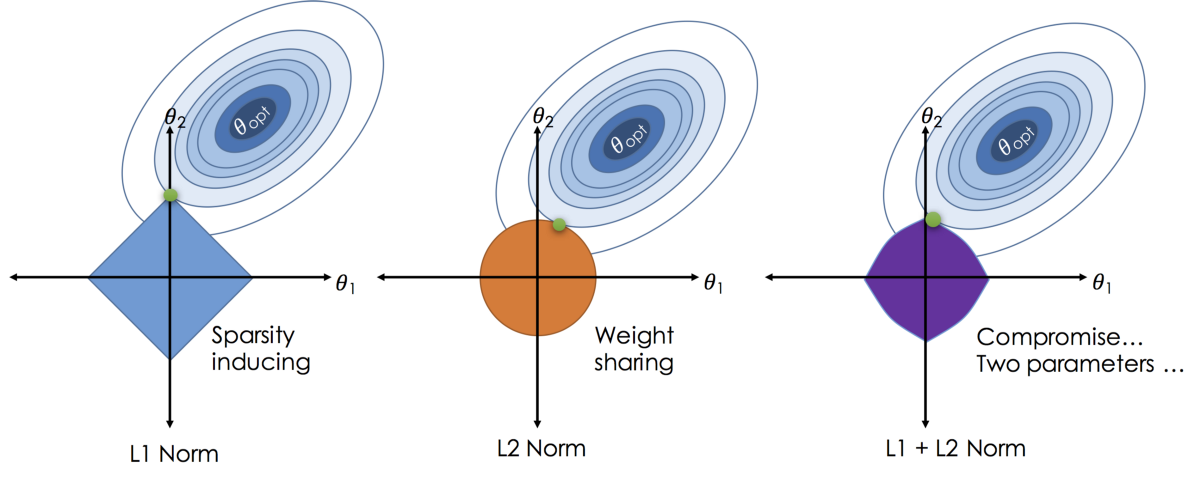
- 릿지 회귀, Ridge Regression : 최소 제곱 비용 함수에 가중치의 제곱합을 추가
L2 규제 Penalty
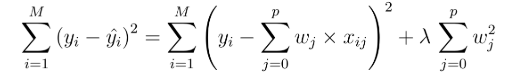
- 라쏘 회귀, Least Absolute Shrinkage and Selection Operator, LASSORegression
L1 규제 Penalty
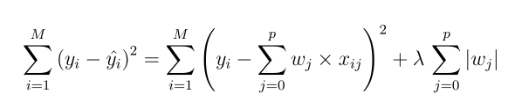
- Elastic Net: L1, L2 규제의 조합
이외 지시변수(Indicator), 상호작용(interaction), 변수 선택 등...
참고 머신러닝 교과서 정오표 https://bit.ly/ml-textbook
이번에 선형회귀에서의 용어가 잘못사용되어 정오표에 반영되어있습니다.
단변량 선형회귀-> 단순 선형회귀다변량 선형회귀-> 다중 선형회귀
머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로 목차
머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로 목차
<머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로 Python Machine Learning By Example, 2/E : Implement machine learning algorithms and techniques to build intelligent systems(Paperback, 2nd Edition)..
potato-potahto.tistory.com
'Data > ML' 카테고리의 다른 글
| Anaconda 설치, 업데이트, 가상환경 (0) | 2021.07.07 |
|---|---|
| 분류모델 성능 지표 (0) | 2021.06.29 |
| 8. 감정분석 (0) | 2021.06.15 |
| 7. 앙상블 학습 (Ensemble Learning) (0) | 2021.06.14 |
| 6. 모델 평가와 하이퍼파라미터 튜닝(미세조정) (0) | 2021.06.14 |