인공신경망 (Artificial Neural Network, ANN)
두뇌를 구성하는 신경학적 신경망을 모티브로 만든 기계학습 모델
순방향 신경망(Feedforward Neural Network)
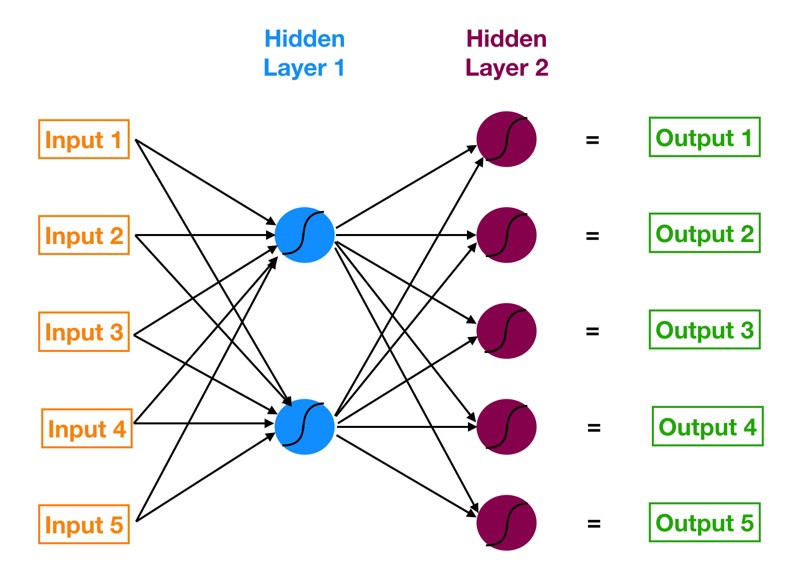
최초이자 가장 간단한 신경망 모델로 항상 입력에서 출력으로 한 방향으로 움직임
- single-layer : 입력- 출력층
- multi-layer 입력, 1개이상의 은닉층, 출력층
- 다층 퍼셉트론: 순방향 신경망의 한 종류로 매개 변수(가중치)를 직접 선정해야함
- 최소 2개 이상의 레이어:은닉층(hidden layer), 출력층(output layer)
- 각 층에서 비선형 활성화 함수 사용
- 학습을 위해서 오차 역전파 Backpropagation 사용 <추후 다룰 예정>
- 신경망: 입력값 데이터를 적절한 값으로 자동으로 학습
- 다층 퍼셉트론: 순방향 신경망의 한 종류로 매개 변수(가중치)를 직접 선정해야함
신경망 학습(Learning) 과정
주어진 훈련 데이터에서 패턴(규칙성)을 찾아서 매개변수(가중치, 편향) 자동 계산
즉, end-to-end machine Learning 종단간 기계학습 : 데이터 입력부터 출력까지 사람 개입 없음
- 역전파 backpropagation : 파라미터에 대한 그레디언 디센트 계산
- 지표: 손실 함수(Loss Function) 최소화
- 방법: 경사법
1) 데이터에서 학습
- 훈련 데이터를 통해 학습하여 최적의 매개변수 찾아냄
- 시험 데이터로 훈련 모델의 범용능력 평가( 이전에 학습하지 않은 새로운 데이터에서도 얼마나 좋은 성능을 내는지)
- 지나치게 학습 데이터에 최적화되는 과적합(overfitting) 줄임
2) 손실 함수(Loss Function)
목표 : 신경망의 최적 매개 변숫값 탐색 시 지표로 손실 함수 최소화(해당 모델의 성능의 나쁨 정도를 나타냄)
미분(기울기)을 이용하여 서서히 갱신 과정을 반복함
- 음수 가중치가 양의 방향으로 변화(계속해서 갱신) 손실 함수 최소화
- 양수 가중치가 음의 방향으로 변화(계속해서 갱신) 손심함수 최소화
- 0 갱신을 멈춘다.
- 평균 제곱 오차 MSE(Mean Squared Error): 실제 예측값과 정답 간의 차이의 평균
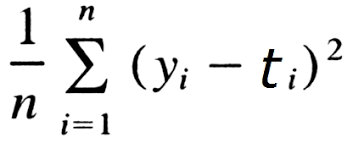
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)- 교차 엔트로피 CEE(Cross-Entropy Error)

# 1Xn 리스트 인경우
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
#미니 배치
def cross_entropy_error(y, t):
# 1차원 리스트인 경우 shape 바꿈
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_sizey= 1, E=0 : 100%이므로 에러 0
y-> 0, E값 - 부호 때문에 점점 커짐
y=0 E=-inf :계산 불가하므로 0보다는 큰 아주 작은 값으로 대체해야 함 예. 0.001
- y:출력 값(추정 값)으로 확률(연속 값)
- t:레이블로 One-hot Encoding(정답인 값에만 1 나머지는 0인 벡터)
- k, i :차원수
두 식 모두 추정 결과값(오차값)이 작을수록 정답에 가까움.
t = [0,0,1,0,0,0,0,0,0,0]
y1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0] #정답
y2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0] #오답
#정답 맞는경우
print(mean_squared_error(np.array(y1), np.array(t)))
# >>> 0.0975
print(cross_entropy_error(np.array(y1), np.array(t)))
# >>> 0.518
#오답인 경우 정답에 비해서 크기가 큼
print(mean_squared_error(np.array(y2), np.array(t)))
# >>> 0.5975
print(cross_entropy_error(np.array(y2), np.array(t)))
# >>> 2.3025
정확도가 아닌 왜 손실 함수일까??
손실 함수는 연속적인 값으로 가중치 매개변수가 조금씩 바뀌게 되면 그에 따른 연속 전 변화(기울기 값) 계산 가능
하지만 정확도( 정답/ 전체 데이터)는 이산적인 값으로 약간의 매개변수 변화에 민감하게 반응하지 않아서 기울기=0을 이용하는 것은 무의미
예시로 스텝 함수와 시그모이드 함수 비교
스텝함수
미분 f'(x)= 0 for x≠0

0 제외하고는 모두 기울기=0이므로 무용
시그모이드 함수
출력층에 이진 분류에 적합

각 값 위치마다 기울기(접선)의 값이 다르며 양 단 끝 값에서 0으로 수렴하는 것을 알 수 있다.
Symmetry point : 미분 값이 가장 큰 부분 0.5
활성화 함수로 적합
경사 법 기울기를 계산 낮은/높은 방향으로 반복해서 이동하여 최솟값(기울기=0)/최댓값에 도달
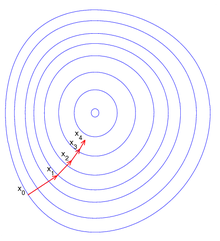
경사 하강법(Gradient descent)
#f:최적화 함수, init_x초기값, lr=학습률 0~1 사잇값,step_num 기울기에 학습률을 곱한 값을 갱신하는 횟수
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f, x)
x -= lr * grad
return x
#f(x0,x1) = x0^2 + x1^2
def function_2(x)
return x[0]**2 +x[1]**2
init_x = np.array ( [-3.0, 4.0])
gradient_descent(function_2, init_x=init_x, lr=0.01, step_num=100)
# >>> [-6.1110793e-10, 8.14814391e-10])
#거의 (0,0) 에 가까움하이퍼파라미터
학습률(Learning rate) η(eta)
한 번의 학습으로 얼마큼 학습하는지 (매개 변숫값이 얼마나 갱신하는지) 반복
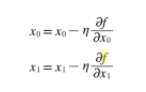
크기 : 직접 설정해야 하는 학습률 크기는 가장 잘 학습하는 최적 값을 찾아야 함.
- 너무 작음: 갱신 안 하고 끝나는 경우 있으며 local minima에 빠지는 경우 있음
- 너무 큼: 발산
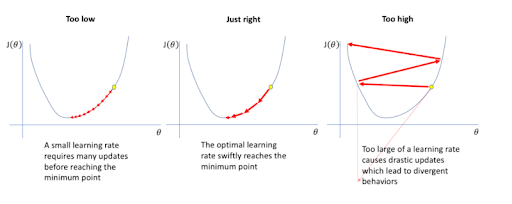
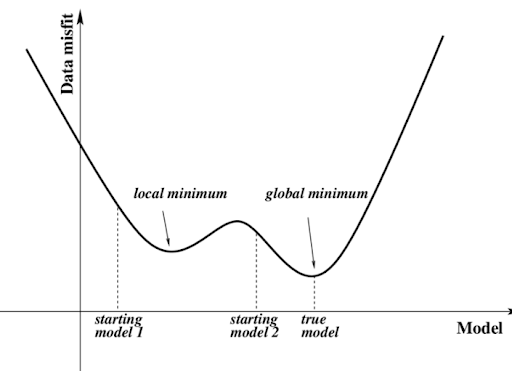
Critical Point (임계정) : 도함수가 0(접선 기울기=0)이 되는 부분
- 극소값 global minima
복잡한 함수에서는 이와 같은 것도 적용 안됨
예. z=x ^2 −y^ 2의 그래프
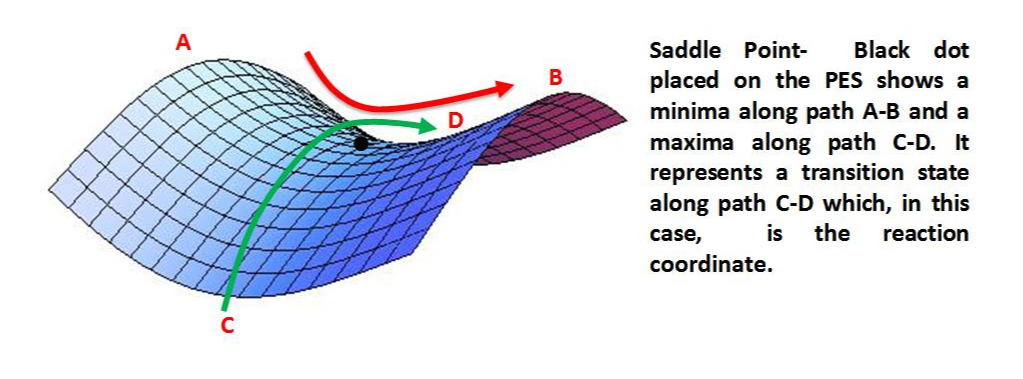
A-B:검은 점이 global minimum
C-D: 검은점이 maxima
학습 알고리즘:확률적 경사 하강법(Stochatic Gradient Descent, SGD)
- 미니 배치: 데이터를 확률적으로 무작위로 추출
- 기울기 산출 - 손실 함숫값 최소화
- 확률적 경사 하강법을 기울기 방향으로 매개변수 갱신
- 반복
2층 신경망 구현(TwoLayerNet) :은닉층 1개
앞서 나온 신경망의 순전파 처리 구현과 공통되는 부분이 많음
import sys, os
sys.path.append(os.pardir)
from common.functions import *
from common.gradient import numerical_gradient
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size,
weight_init_std=0.01):
# 가중치 초기화
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 현재 가중치와 편향으로 출력값 예측
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# 교차 엔트로피 오차 계산
# x : 입력 데이터, t : 정답 레이블
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
# 정확도 계산
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis = 1)
t = np.argmax(t, axis = 1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# 이미 정의된 함수 numerical_gradent를 이용하여 입력값 x에서의 손실함수의 기울기 계산
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads

미니 배치 학습
미니 배치:데이터중 랜덤 하게 일부만 추출하여 학습 (표본추출과 동일)
이유: 데이터가 많은 경우 표본을 통해 모수의 근사치로 사용
미니 배치 100개의 데이터를 바탕으로 확률적 경사 하강법 수행해 매개변수 갱신
갱신 횟수 1만 번 설정, 손실 함수 계산,
import numpy as np
from dataset.mnist import load_mnist
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
train_loss_list = []
# 하이퍼파라미터
iters_num = 1000 # 반복 횟수
train_size = x_train.shape[0]
batch_size = 100 # 미니배치 크기
learning_rate = 0.1
network = TwoLayerNet(input_size = 784, hidden_size = 50, output_size = 10)
print("시작")
for i in range(iters_num):
# 미니배치 획득
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
grad = network.numerical_gradient(x_batch, t_batch)
# 매개변수 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
print('갱신')
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
추론(Inference & Reasoning) 과정: 학습된 매개변수 사용하여 학습에 사용되지 않은 새로운 입력 데이터 분류
- 순 전파 forward propagation : 신경망 모델의 입력층에서 출력층까지의 순서대로 변수 계산
추론의 정도는 정화도 등의 여러 지표를 이용하여 비교
신경망의 추론 처리
입력층 크기: 이미지 데이터 크기 (가로*세로)
출력층 크기: 분류 개수
배치 처리
배치 batch: 모델 학습의 반복 1회(경사 업데이트 1회)에 사용되는 하나로 입력 데이터 묶음
배치 크기 : 하나의 배치에 포함된 입력 데이터 예의 수
- 컴퓨터 계산 시 이미지 1장당 처리시간 감소 ( 큰 배열 처리가 분할된 작은 배열 여러 번 처리하는 것보다 효율적 )
배치 정규화 (normalization) : 배치 단위로 활성화 함수 출력 값을 정규화
이미지라면 0~255(pixel 값) -> 0~1 사이 값으로 변환
Reference
밑바닥부터 시작하는 딥러닝(Deep Learning from Scratch)
'Data > AI' 카테고리의 다른 글
| Deep Learning(딥러닝) - 4.오차역전파(Error Backpropagation) (0) | 2021.10.17 |
|---|---|
| Deep Learning(딥러닝) - 3.활성화 함수(Activation Function) (0) | 2021.10.16 |
| Deep Learning(딥러닝) - 1.딥러닝의 역사와 Perceptron(퍼셉트론) (0) | 2021.10.13 |
| [Python] 파이썬 시작하기(파이썬, 아나콘다,주피터 노트북 다운로드 설치, 실행) (0) | 2021.08.27 |
| Anaconda 설치, 업데이트, 가상환경 (0) | 2021.07.07 |