4. 서포트 벡터 머신(Support Vector Machine)을 사용한 최대 마진 분류
keywords: Margin, Penalty, Mapping(kernel)

- 마진 (margin): 클래스를 구분하는 초평면과 이 초평면에서 가장 가까운 훈련 샘플 사이의 거리
- 서포트 벡터(Support vectors): 초평면(hyperplane, 3차원 속의 평면을 일반화하여 부름)에서 가장 가까운 샘플들
- 페널티 (Penalty ξ): applied for each contaminant error inside the margin and the sum of all such errors is minimized to get the best separation.( tolerance for misclassification)
- Convex Hull: 각 클래스의 바깥 경계로 이 경계
- Objective: 마진을 최대화하는 결정 경계(max Margin, min Penalty)는 일반화 오차가 낮아지는 경향

5. 커널 SVM (Kernel SVM)을 사용하여 비선형 문제 풀기
1) 선형적으로 구분되지 않는 데이터(비선형 데이터 예. XOR)를 위한 커널 방법
Kernel Method: 비선형 데이터에서 매핑함수를 사용하여 원본 특성의 비선형 조합을 선형적으로 구분되는 고차원 공간에 투영하는 것
2차원 데이터셋을 새로운 3차원 특성 공간(Feature Space)으로 변환(고차원 공간)하여 두 클래스를 구분하는 선형(분할) 초평면은 원본 특성 공간으로 되돌리면 비선형 결정 경계 형성

2)커널 기법을 사용하여 고차원 공간에서 분할 초평면 찾기
- 앞에서 훈련 데이터를 고차원 특성 공간으로 변환한 후 데이터를 분류하는 선형 SVM모델 훈련
- 매핑 함수 사용하여 새로운 데이터를 변환하여 분류
:( 새로운 특성을 만드는 계산 비용(high cost of computation)이 높음(특히, 고차원 데이터 : 특성 많은 경우) <콰드라틱 프로그래밍 문제 >
커널 함수(kernel function) : 높은 계산 비용 절감, 두 포인트의 내적
- 방사 기저 함수(Radial Basis Function, RBF)
- 가우시안 커널(Gaussian Kernel)
커널: 샘플간의 유사도 함수(similarity funciton)로 음수 부호가 거리 측정을 유사도 점수로 바꾸는 역할을 함
지수 함수로 얻게 되는 샘플 유사도 점수 : (0 , 1)
매개변수 (C, gamma)
- Cost(C) : 페널티(얼마나 많은 데이터 샘플이 다른 클래스로 놓여지는지)를 얼마나 허용하는지 결정
- C의 유무에 따라 하드마진(Hard Margin), 소프트 마진(Soft Margin)으로 나뉨
- 큰 C 값에서는 이상치가 존재할 가능성을 작게 분류하여 데이터에 민감하게 반응하게 됨(과대 적합 현상 발생)

- Gamma: 가우시안 구(Gaussian Sphere)의 크기를 제한하는 매개변수로 이해 가능, 클수록 SV의 영향, 범위 줄어듦( 결정 경계가 더 민감해짐= 구불구불해짐)

-> Grid Search: 두 매개 변수의 조합을 테스트해거 가장 좋은 선능을 내는 매개변수를 찾아냄(경험적 방법)
(1) 데이터 시각화
import matplotlib.pyplot as plt
import numpy as np
#xor 문제를 만들어 약 100개 샘플은 레이블 1 나머지 100개는 -1 할당
np.random.seed(1)
X_xor = np.random.randn(200, 2)
y_xor = np.logical_xor(X_xor[:, 0] > 0,
X_xor[:, 1] > 0)
y_xor = np.where(y_xor, 1, -1)
plt.scatter(X_xor[y_xor == 1, 0],
X_xor[y_xor == 1, 1],
c='b', marker='x',
label='1')
plt.scatter(X_xor[y_xor == -1, 0],
X_xor[y_xor == -1, 1],
c='r',
marker='s',
label='-1')
plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.legend(loc='best')
plt.tight_layout()
plt.show()
위의 그래프를 보면 양성(1)과 음성(-1) 클래스를 선형 초평면으로 구분할 수없음. 따라서 커널 방법에서 매핑 함수 사용하여 고차원 공간.(예. 2차 워 ->3차원 변환 구분)을 원본 특성 공간으로 되돌리면 비선형 결계가 됨.

(2) 고차원 공간에서 비선형 데이터 ( XOR ) 초평면 찾기 (훈련)
- C=10, Gamma=0.1인 경우
svm = SVC(kernel='rbf', random_state=1, gamma=0.10, C=10.0)
svm.fit(X_xor, y_xor)
plot_decision_regions(X_xor, y_xor,
classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()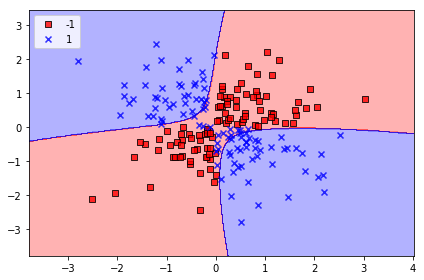
- C=1, Gamma 0.2인 경우
svm = SVC(kernel='rbf', random_state=1, gamma=0.2, C=1.0)
svm.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined,
classifier=svm, test_idx=range(105, 150))
plt.scatter(svm.dual_coef_[0,:], svm.dual_coef_[1,:])
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
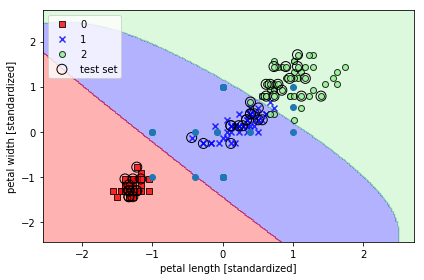
- C=1, Gamma =100인경우
svm = SVC(kernel='rbf', random_state=1, gamma=100.0, C=1.0)
svm.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined,
classifier=svm, test_idx=range(105, 150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()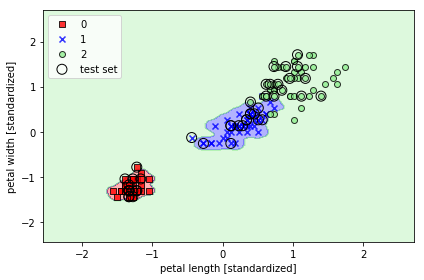
Gamma = 0,2인 경우는 세개로 분류하는 데 있어서 선형에 가깝게 분류했지만 100인 경우 값들과 결정 경계가 가까움(과대 적합)
6. 결정 트리(Decision Tree) 학습
Keywords: 가지치기(Pruining), 정보이득(IG), 불순도 지표 , 랜덤포레스트(Random Forest)
이해하기 가장 쉬우며 직관적인 머신러닝 방법으로 설명이 중요한 경우에 사용하며 input은 수치,범주 모두 가능
- 훈련 데이터에 있는 특성을 기반으로 샘플의 클래스 레이블 추정할 수 있는 일련의 질문들을 학습
- 트리의 뿌리(root)에서 시작해서 정보 이득(Information Gain, IG) 최대가 되는 특성으로 분할
- 나뭇잎 노드(Leaf node)에서 순도 높아질 때까지 모든 자식 노드에서 위의 분할 작업 반복
- 각 노드의 모든 샘플은 동일한 클래스에 속함
:( 뿌리의 깊이(depth)가 깊어질수록(복잡한 경계) 순도 높아지나 과대 적합 가능성이 높아짐.
->가지치기(Pruning) -트리의 최대 깊이 제한하여 과적합 방지
매개변수
- 최대 허용 깊이 D: 하나의 트리의 뿌리부터 각 노드의 층을 거쳐서 마지막 노드까지 몇개의 층을 거칠것인지 결정. 깊이가 깊으면 과대적합 현상의 위험
- 훈련목적함수: 노드를 분할시 정보 이득 최대화(Maximize IG)
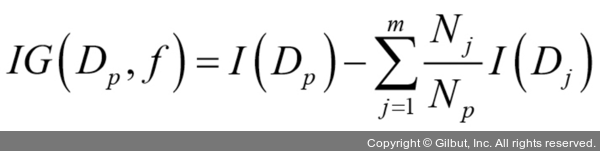
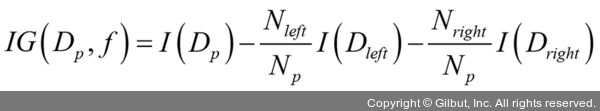
- f: 분할에 사용하는 특성
- Dp, Dj: 부모와 j번째(이진트리인 경우 왼쪽,오른쪽) 자식 노드의 데이터 셋
- I: 불순도(Impurity) - 낮을수록IG 커짐
- Np: 부모 노드에 있는 전체 샘플 갯수
- Nj: j 번째 자식 노드에 있는 샘플 개수
부모노드의 분순도와 자식 노드의 불순도 차이
- 노드 분할 함수 : 이진 결정 트리의 분할 조건, 불순도 지표
- 지니 불순도(Gini Impurity , Ig) : 오분류 될 확률 최소화
- 엔트로피 (entropy, IH) : 상호 의존 정보 최대화( 이진 클래스 인 경우 균등 분포시 1, 완벽 분류 0)
- 분류 오차( Classification Error, Ie) : DT 에 권장 되지 않음( 노드의 클래스 확률 변화에 덜 민감)
( 이진 클래스 인 경우 균등 분포시 1, 완벽 분류 0)
import matplotlib.pyplot as plt
import numpy as np
#3가지 불순도 기준 시각적 비교하기
def gini(p):
return p * (1 - p) + (1 - p) * (1 - (1 - p))
def entropy(p):
return - p * np.log2(p) - (1 - p) * np.log2((1 - p))
def error(p):
return 1 - np.max([p, 1 - p])
#class 1 확률 범위 0,1 로 지정하고 스케일 조정
x = np.arange(0.0, 1.0, 0.01)
ent = [entropy(p) if p != 0 else None for p in x]
sc_ent = [e * 0.5 if e else None for e in ent]
err = [error(i) for i in x]
fig = plt.figure()
ax = plt.subplot(111)
for i, lab, ls, c, in zip([ent, sc_ent, gini(x), err],
['Entropy', 'Entropy (scaled)',
'Gini Impurity', 'Misclassification Error'],
['-', '-', '--', '-.'],
['black', 'lightgray', 'red', 'green', 'cyan']):
line = ax.plot(x, i, label=lab, linestyle=ls, lw=2, color=c)
ax.legend(loc='upper center', bbox_to_anchor=(0.5, 1.15),
ncol=5, fancybox=True, shadow=False)
ax.axhline(y=0.5, linewidth=1, color='k', linestyle='--')
ax.axhline(y=1.0, linewidth=1, color='k', linestyle='--')
plt.ylim([0, 1.1])
plt.xlabel('p(i=1)')
plt.ylabel('Impurity Index')
plt.show()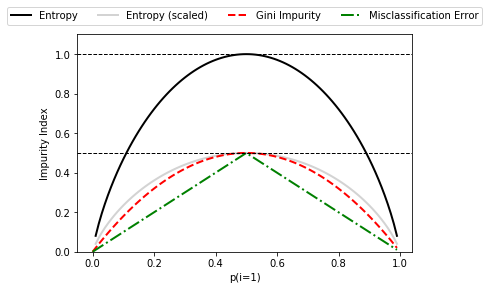
지니불순도, 최대 깊이 4 인 경우
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(criterion='gini',
max_depth=4,
random_state=1)
tree.fit(X_train, y_train)
X_combined = np.vstack((X_train, X_test))
y_combined = np.hstack((y_train, y_test))
plot_decision_regions(X_combined, y_combined,
classifier=tree, test_idx=range(105, 150))
plt.xlabel('petal length [cm]')
plt.ylabel('petal width [cm]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()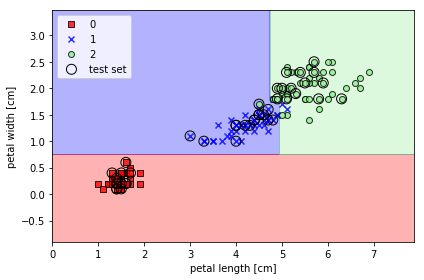
특성 공간을 사각 격자로 나누기 때문에 복잡한 결정 경계 만들기 가능하다
Petal Width =0.75를 기준으로 분할되고 0.75 이상인 경우 Petal Length가 4.75 기준으로 나누어 졌다. 따라서 테스트 세트를 앞에 말한 기준으로 0= Setosa, 1= Versicolor, 2= Virginica 클래스로 나누었다. 클래스 0은 다른 클래스들에 비해서 불순도 지표가 낮을것으로 예상되어진다.
3) 랜덤 포레스트(Random Forest)로 여러개의 결정 트리 연결
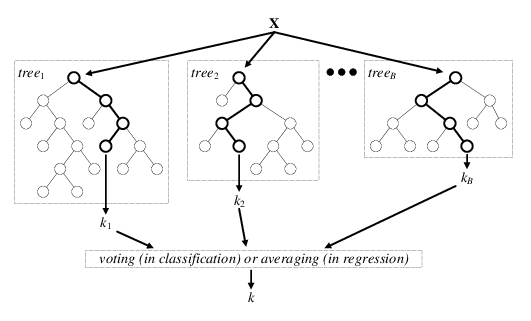
- 앙상블 학습 방법(Ensenble Learning Method): 머신 러닝 모델의 성능 향상을 위해서 다수의 학습 알고리즘 사용,결합하여 일반화 가능
- weak learner:개별 학습된 모델
- 랜덤포레스트(Random Forest): 앙상블 학습 방법의 하나로 훈련과정에서 추출한 다수의 결정트리로부터 다수결 투표나 평균치를 내어 분류나 회귀에 사용.
- 선능 변동폭이 큰( 분산) DT의 단점을 랜덤 노드 최적화(randomized node optimization) or Bagging (Bootstrap AGGregatING)으로 보완
- 사이킷런은 사후가지치기가 없으므로 앙상블 방법으로 과적합 위험 줄임
- 결정 트리는 최선의 분할을 찾기위해서 모든 특성 평가하게됨.
Steps
- 중복 허용하여 n개의 랜덤한 Bootstrap샘플을 뽑음
- 결정트리 학습 (중복허용하지않은 랜덤 샘플링( d개의 특성 선택) , 정보이득과 같은 목적 함수 기준으로 최선의 분할을 만드는 특성을 사용 노드 분할)
- 1.2번 k번 반복
- 각 트리의 예측을 모아 다수결 투표(majority voting) 로 클래스 레이블 할당
- 트리 갯수(샘플 크기 n) 와 계산비용, 분류기 성능(편향-분산 tradeoff) 비례(과대적합 가능성 비례)
- :) 하이퍼파라미터 튜닝에 노력 많이 안기울여도 됨,
7. k-최근접 이웃(K-Nearesrt Neighbor, KNN): 게으른 학습( Lazy Laerner) 알고리즘
- 모수 모델(Parametric Model):새로운 데이터 포인트 분류할 수 있는 판별 함수를 학습하기 위해 훈련 데이터셋에서 모델 파라미터 추정,
- eg. Perceptron,로지스틱 회귀, 선형 SVM
- Eager Learner: training 데이터로 학습한 모델로
- 비모수 모델(Nonparametric Model): 고정된 개수의 파라미터로 설명될 수 없으며 훈련 데이터가 늘어남에 따라 파라미터도 증가
- 예. 결정 트리, 랜덤 포레스트, 커널 SVM, KNN
- 인스턴스 기반 모델(instance based model)은 훈련 데이터셋을 메모리에 저장
- Lazy Learner : 알고리즘이 학습하는 대신 훈련 데이터셋을메모리에 저장한 모델로 가장 가까운 데이터(instanvce)와 비교하여 레이블링 함. 메모리 기반 방식의 분류기는 학습 과정 비용 없음
훈련 후 원본 훈련 데이터셋이 불필요함.
훈련 후 원본 훈련 데이터셋이 불필요함.
- :) 새로운 훈련 데이터 즉시 적용가능, 견고함
- :( 새로운 샘플을 분류하는 계산 복잡도
- :( 훈련 단계가 없어 훈련 샘플을 버릴 수 없음
- :( 대규모 데이터셋에서 작업 시 저장 공간 문제 생김
- :( 가장 가가운 데이터셋이 이상치인 경우 오분류
KNN 알고리즘
- 정수 k & 거리 측정 기준 선택
- 분류하려는 샘플에서 k개의 최근접 이웃 찾음
- 다수결 투표(Majority Voting)를 통해 클래스 레이블 할당: 선택한 거리 측정 기준에 따라서 분류하려는 포인트 * 다수결 투표가 동일한 경우 사이킷런의KNN은 거리가 더 가까운 이웃을, 거리가 동일한 경우 먼저 나타난 샘플의 클래스 레이블 선택.
- 적절한 K를 선택은 <no golden rule!>. 너무 작은 숫자를 선택하면 과대 적합, 큰 숫자 선택 시 과소 적합됨.
- 특성에 알맞은 거리 측정 지표 선택 필요:
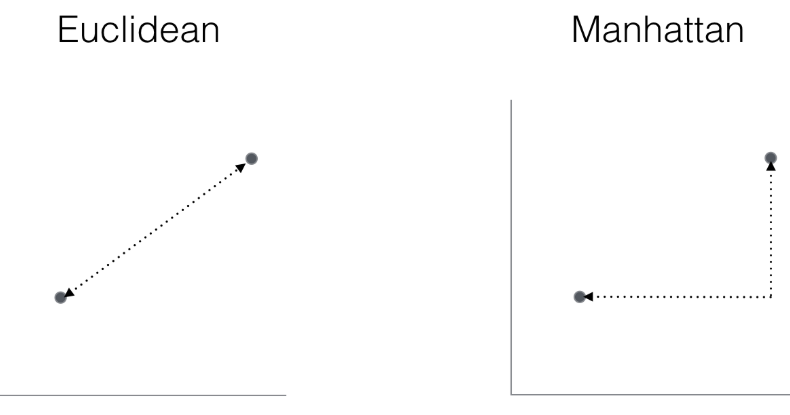
- Euclidean: 두 사이의 가장 가까운 직선 거리 ( 특성이 동일하게 취급되도록 표준화 필요)
- 피타고라스의 정리에서 두 벡터 사이거리(직각 삼각형의 빗변)은 각 직각변의 제곱의 합에 제곱근을 한것과 동일함을 이용
- Manhattan : Taxicab Geometry라고도 불리며 맨해튼의 거리가 격자로 되어있어 택시가 가는 경로와 비슷하다하여 지어졌고 직교 좌표계(Cartesian Coordinate)에서 두 지점의 좌표의 차이의 절대값의 합이다.
- 예. (0,0) 에서 (1,1)사이의 거리 측정
- Euclidean : squareroot( (0-1)^2+(0-1)^2 ) = squaresroot (2)
- Manhattan: |0-1| +|0-1|=2
- Euclidean: 두 사이의 가장 가까운 직선 거리 ( 특성이 동일하게 취급되도록 표준화 필요)
- 과대 적합을 피하기 위해서 규제를 적용할 수 없으므로 특성 선택, 차원 축소 기법 사용하여 차원의 저주(the curse of dimenstionality : 데이터셋의 차원이 늘어나면서 특성 공간이 점점 희소(sparse) 해지는 현상) 피함
거리 측정 지표에대한 설명과 중요성에대한 자세한 내용은 다음 블로그 참고: Eucliean, Mahattan ,Minkowski...
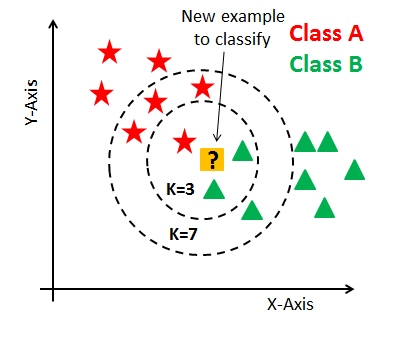
예를 들어 위의 그림에서 k=3인 경우 majority voting을 통해서 삼각형이 별 모양보다 더 많으므로 class B로 분류되지만 k=7인 경우 별이 4개고 삼각형이 3개이므로 ClassA로 클래스 레이블 할당( 예측)한다.
요약
- 선형, 비선형 문제에 적절한 머신 러닝 알고리즘 선택
- 결정 트리 - 모델 해석이 중요한 경우
- 로지스틱 회귀: 확률적 경사 하강법 사용 온라인 학습, 특정 이벤트 확률 예측 사용
- SVM: 선형, 비선형(커널 트릭 사용), 하이퍼 파라미터 :C, Gamma
- 앙상블 모델: 랜덤 포레스트, 과대 적합 요소 적음
- KNN분류기 : 게으른 학습 통해 다른 종류의 분류 방식 사용, 모델 훈련 없이 예측 만들지만 계산 비용 높음
- ! 훈련 데이터셋에 있는 가용한 데이터, (정보 풍부하고 판단에 도움되는 특성 있어 좋은 예측 만들어 냄) 다음장에서 전처리,특성 선택, 차원축소 설명
>>>>
책에 나온 내용은 핵심 만 훑어서 다양한 자료 참고 해서 보는데 시간이 좀 걸리게 된다. 매개 변수와 더 자세한 수식 공부할게 많음..
핑크색으로 하이라이트 친 부분 나중에 보충해서 새로운 포스트나 수정할 계획
머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로 목차
머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로 목차
<머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로 Python Machine Learning By Example, 2/E : Implement machine learning algorithms and techniques to build intelligent systems(Paperback, 2nd Edition)..
potato-potahto.tistory.com
Reference
https://ratsgo.github.io/machine%20learning/2017/05/23/SVM/
https://www.datacamp.com/community/tutorials/k-nearest-neighbor-classification-scikit-learn
'Data > ML' 카테고리의 다른 글
| 5.차원축소를 이용한 데이터 압축 (0) | 2021.06.13 |
|---|---|
| 4. 데이터 전처리 (0) | 2021.06.12 |
| 2. 간단한 분류 알고리즘 훈련 (0) | 2021.06.09 |
| 머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로 목차 (0) | 2021.06.08 |
| 1. 컴퓨터는 데이터에서 배운다. (0) | 2021.06.07 |