특성 추출(feature extraction):원본 특성 중에서 가장 중요한 일부 추출( 데이터 압축)
저장 공간 절약학습
알고리즘 계산 효율성 향상
예측 성능 향상
>특성 선택 알고리즘 이용:전진선택법,후진소거법,양방향 선택법
5 장 . 차원축소(dimension reduction): 데이터의 특성들을 새로운 특성으로 변환하면서 원본 특성 유지
1. 선형 변환 기법
- 비지도 학습: PCA 주성분 분석 (find patter without reference)
- 지도 학습: LDA선형 판별분석
2. 비선형 변환 기법
- 커널 PCA(Kernel Principal Component Analysis, KPCA)
5. 1. 비지도 학습 : 주성분 분석 (Principal Component Analysis,PCA)
분산이 최대인 직교하는 특성축을 따라서 동일 혹은 저 차원으로 투영(새로운 공간의 직교 좌표)

단계

- x,y: 원 데이터 특성 축
- v,u: 주성분(Principal compnent): 원성분들의 선형결합
관측값과 주성분 (PC) 사이의 직각 거리(perpendicular distnace) 최소화
- N차원을 M차원으로 매핑하는 행렬(N<<M) W
- PC1(주성분): 가장 큰 분산 갖음, 가장 작은 error(선과 관측값간의 수직 거리)
- 특성 사이의 상관관계 기반으로 데이터 특성을 잡아냄
응용:탐색적 데이터분석(EDA), 잡음제거, 특성이 많은 데이터분야(생명공학 Genes)


단계
제약: 모든 주성분은 다른 주성분들과 상관관계가 없다(직교 orthogonal)'
1). 다른 스케일인 데이터 표준화(평균 =0) : 스케일에 민감 X
2). 공분산 행렬(covariance matrix)생성(정방 대칭 행렬) X^tX

- i<>j:공분산
- 각 특성의 변동의 닮은 정도 (같이 변한는 정도 :같이 증감하는지 증가하고 감소하는지)
- 선형 변환을 통해서 정규분포를 shearing 함
- 샘플의 수가 증가하면 공분산도 커짐 -
3). Eigendecomposition(고유값 분해) : 공분산 행렬 d개의 고유벡터(Eigen Vector)와 고유값(Eigen Value)으로 분해
- 고유벡터: 선형변환의 주축 (sheering해도 크기, 방향 유지,최대 분산 )
- 고유값 : 주성분의 크기고윳값을 내림차순으로 정렬하고 고유 벡터 순위 매김 -> 주성분 추출됨

4). 고윳값이 가장 큰 K개의 고유 벡터 선택(K : 새로운 특성 부분 공간의 차원 K<= d)
- 가장 큰 분산(많은 정보)를 가진 k개 고유벡터(PC) 선택
- 고유값( 고유벡터 크기)내림차순 정렬
- 고유값의 설명된 분산(explained variance) 비율은 PC1> PC2> ... PC k
5). 특성 변환 : 상위 k개의 고유벡터로 투영 행렬(projection matrix)W만듦
6). XW=A 특성 부분 공간으로 변환

제한
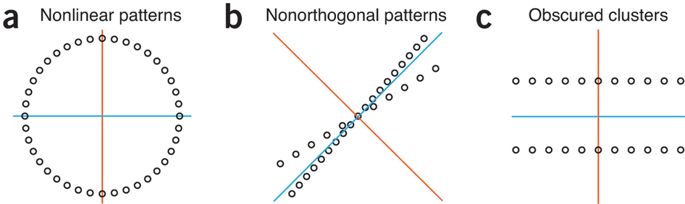
a. 비선형 패턴
b. 매우 높은 상관관계의 데이터
c. 분산을 최대화하는 것이지 클러스터링이 아님
5.2 지도 학습 : 선형 판별 분석(Linear Discriminant Analysis,LDA)
데이터 분포를 이용하며 클래스를 최적으로 구분할 수 있는 특성 부분 공간 찾기
TMI : Fisher's LDA
이진 분류 문제 위해서 선형 판별 공식 고안 _ 클래스 공분산 동일, 정규분포 따른다는 가정
가정:
- 데이터는 정규분포를 따름
- 클래스가 동일한 공분산 행렬을 가짐
- 샘플은 서로 통계적으로 독립적
각 클래스별 평균 사이가 멀고 분산이 작아야함
단계
- 데이터셋 표준화
- 각 클래스에 대해 평균 벡터 계산
- 클래스간의 산포 행렬(Scatter matrix)와 클래스 내 산포 행렬 구성
- 두 행렬의 고유 벡터와 고윳값 계산
- 고윳값을 내림차순 정렬
- 최상위 k개의 고유벡터 선택 d*k 차원의 변환행렬W(열=고유 벡터)
- 샘플을 새로운 특성 부분 공간으로 투영
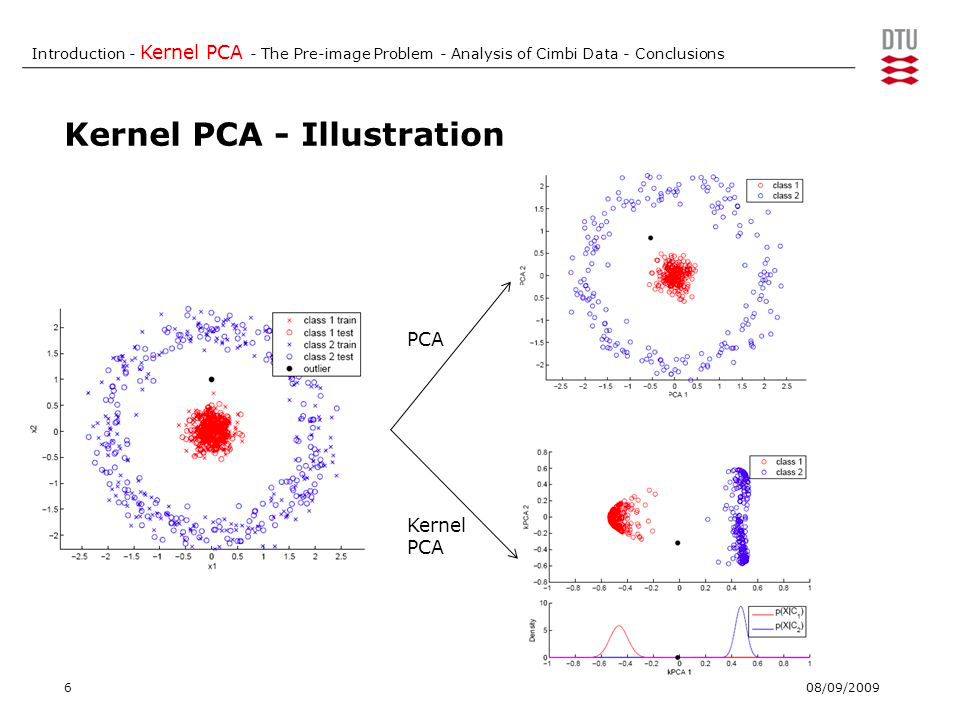
5.3. 비선형 문제 : 커널PCA (KPCA)
비선형 데이터를 선형 분류기에 적합한 새로운 저차원 부분 공간으로 변환하여 선형적 구분 (Kernel SVM과 비슷)
커널 함수
비선형 매핑 함수 정의 ( 베른하르트 슐코프 Bernhard Scholkopf)
- 다항 커널
- theta: 임계 값
- P: 사용자 지정 거듭제곱
- 하이퍼볼릭 탄젠트(Hyperbolic Tangent, sigmoid) 커널
- 방사기저 함수(Radial Basis Function, RBF) or Gaussian kernel
커널 트릭: 원본 특성 공간에서 두 고차원 특성 벡터의 유사도 계산
단계
- 커널(유사도)핼렬 K계산
- 표준화커널 행렬 중앙에 맞춤
- 고유값 크기대로 내림차순 정렬
- 최상위 k개의 고유벡터 고름
새로운 데이터 포인트 투영
머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로 목차
머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로 목차
<머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로 Python Machine Learning By Example, 2/E : Implement machine learning algorithms and techniques to build intelligent systems(Paperback, 2nd Edition)..
potato-potahto.tistory.com
Reference
Lever, J., Krzywinski, M. & Altman, N. Principal component analysis. Nat Methods 14, 641–642 (2017). https://doi.org/10.1038/nmeth.4346
https://www.youtube.com/watch?v=jNwf-JUGWgg
https://ratsgo.github.io/machine%20learning/2017/04/24/PCA/
https://ratsgo.github.io/machine%20learning/2017/03/21/LDA/
https://www.dezyre.com/data-science-in-python-tutorial/principal-component-analysis-tutorial
https://stats.stackexchange.com/questions/2691/making-sense-of-principal-component-analysis-eigenvectors-eigenvalues
https://www.nature.com/articles/nmeth.4346
'Data > ML' 카테고리의 다른 글
| 7. 앙상블 학습 (Ensemble Learning) (0) | 2021.06.14 |
|---|---|
| 6. 모델 평가와 하이퍼파라미터 튜닝(미세조정) (0) | 2021.06.14 |
| 4. 데이터 전처리 (0) | 2021.06.12 |
| 3.사이킷런을 타고 떠나는 머신 러닝 분류 모델 투어 (0) | 2021.06.11 |
| 2. 간단한 분류 알고리즘 훈련 (0) | 2021.06.09 |